The probability of data loss in large clusters

Published by Martin Kleppmann on 26 Jan 2017.

This blog post uses MathJax to render mathematics. You need JavaScript enabled for MathJax to work.

Many distributed storage systems (e.g. Cassandra, Riak, HDFS, MongoDB, Kafka, …) use replication to make data durable. They are typically deployed in a “Just a Bunch of Disks” (JBOD) configuration – that is, without RAID to handle disk failure. If one of the disks on a node dies, that disk’s data is simply lost. To avoid losing data permanently, the database system keeps a copy (replica) of the data on some other disks on other nodes.

The most common replication factor is 3 – that is, the database keeps copies of every piece of data on three separate disks attached to three different computers. The reasoning goes something like this: disks only die once in a while, so if a disk dies, you have a bit of time to replace it, and then you still have two copies from which you can restore the data onto the new disk. The risk that a second disk dies before you restore the data is quite low, and the risk that all three disks die at the same time is so tiny that you’re more likely to get hit by an asteroid.

As a back-of-the-envelope calculation, if the probability of a single disk failing within some time period is 0.1% (to pick an arbitrary number), then the probability of two disks failing is (0.001)² = 10^-6, and the probability of all three disks failing is (0.001)³ = 10^-9, or one in a billion. This calculation assumes that one disk’s failure is independent from another disk’s failure – which is not actually true, since for example disks from the same manufacturing batch may show correlated failures – but it’s a good enough approximation for our purposes.

So far the common wisdom. It sounds reasonable, but unfortunately it turns out to be untrue for many data storage systems. In this post I will show why.

It’s so easy to lose data, la la laaa

If your database cluster really only consists of three machines, then the probability of all three of them dying simultaneously is indeed very low (ignoring correlated faults, such as the datacenter burning down). However, as you move to larger clusters, the probabilities change. The more nodes and disks you have in your cluster, the more likely it is that you lose data.

This is a counter-intuitive idea. “Surely,” you think, “every piece of data is still replicated on three disks. The probability of a disk dying doesn’t depend on the size of the cluster. So why should the size of the cluster matter?” But I calculated the probabilities and drew a graph, and it looked like this:

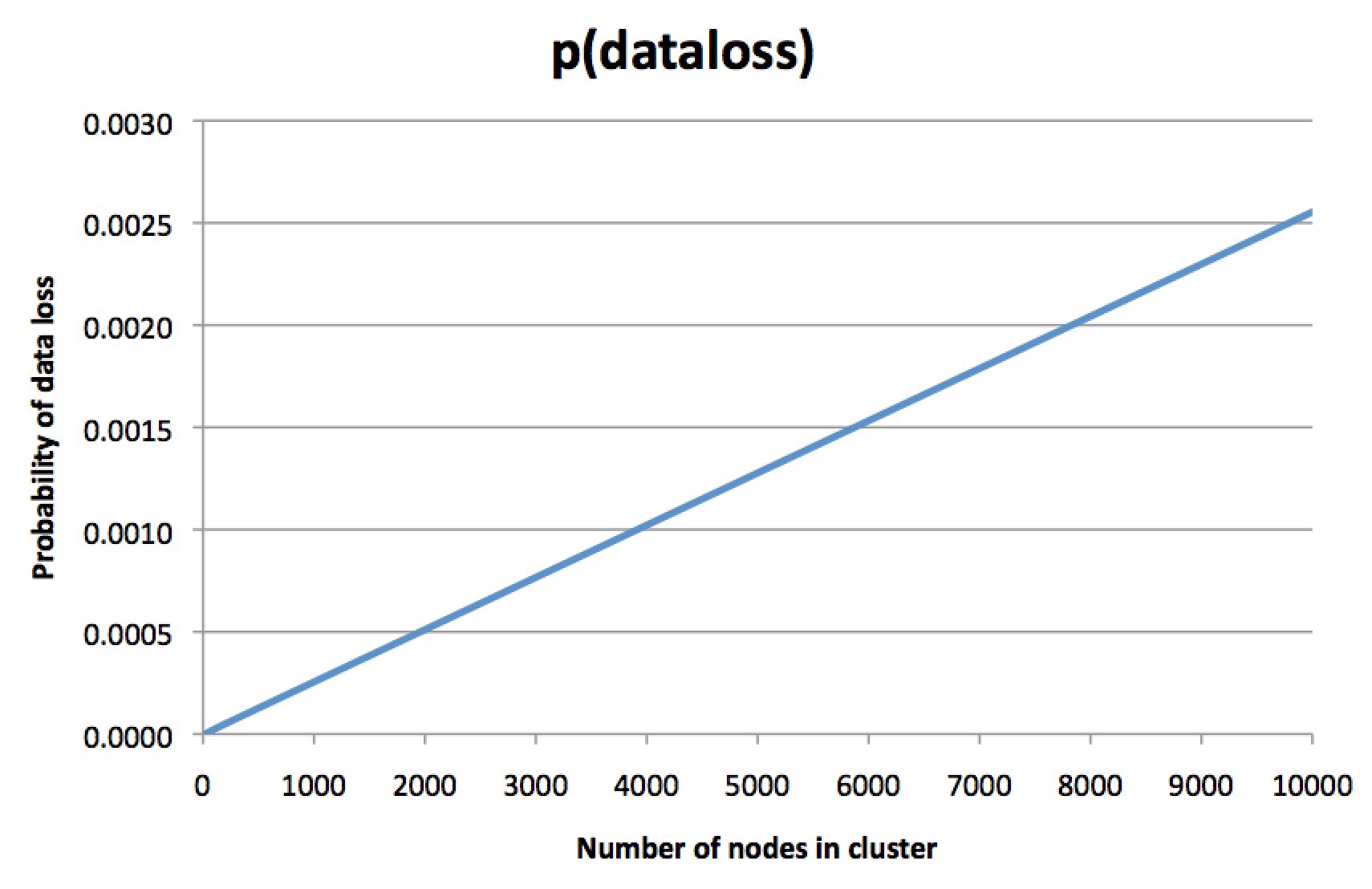
To be clear, this isn’t the probability of a single node failing – this is the probability of permanently losing all three replicas of some piece of data, so restoring from backup (if you have one) is the only remaining way to recover that data. The bigger your cluster, the more likely you are haemorrhaging data. This is probably not what you intended when you decided to pay for a replication factor of 3.

The y axis on that graph is a bit arbitrary, and depends on a lot of assumptions, but the direction of the line is scary. Under the assumption that a node has a 0.1% chance of dying within some time period, the graph shows that in a 8,000-node cluster, the chance of permanently losing all three replicas of some piece of data (within the same time period) is about 0.2%. Yes, you read that correctly: the risk of losing all three copies of some data is twice as great as the risk of losing a single node! What is the point of all this replication again?

The intuition behind this graph is as follows: in an 8,000-node cluster it’s almost certain that a few nodes are always dead at any given moment. That is normally not a problem: a certain rate of churn and node replacement is expected and a part of routine maintenance. However, if you get unlucky, there is some piece of data whose three replicas just happen to be three of those nodes that have died – and if this is the case, that piece of data is gone forever. The data that is lost is only a small fraction of the total dataset in the cluster, but still that’s not great: when you use a replication factor of 3, you generally mean “I really don’t want to lose this data”, not “I don’t mind occasionally losing a bit of this data, as long as it’s not too much”. Maybe that piece of lost data was a particularly important one.

The probability that all three replicas are dead nodes depends crucially on the algorithm that the system uses to assign data to replicas. The graph above is calculated under the assumption that the data is split into a number of partitions (shards), and that each partition is stored on three randomly chosen nodes (or pseudo-randomly with a hash function). This is the case with consistent hashing, used in Cassandra and Riak, among others (as far as I know). With other systems I’m not sure how the replica assignment works, so I’d appreciate any insights from people who know about the internals of various storage systems.

Calculating the probability of data loss

Let me show you how I calculated that graph above, using a probabilistic model of a replicated database.

Let’s assume that the probability of losing an individual node is \(p=P(\text{node loss})\). I am going to ignore time in this model, and simply look at the probability of failure in some arbitrary time period. For example, we could assume that \(p=0.001\) is the probability of a node failing within a given day, which would make sense if it takes about a day to replace the node and restore the lost data onto new disks. For simplicity I won’t distinguish between node failure and disk failure, and I will consider only permanent failures (ignoring crashes where the node comes back again after a reboot).

Let \(n\) be the number of nodes in the cluster. Then the probability that \(f\) out of \(n\) nodes have failed (assuming that failures are independent) is given by the binomial distribution:

\[ P(f \text{ nodes failed}) = \binom{n}{f} \, p^f \, (1-p)^{n-f} \]

The term \(p^f\) is the probability that \(f\) nodes have failed, the term \((1-p)^{n-f}\) is the probability that the remaining \(n-f\) have not failed, and \(\binom{n}{f}\) is the number of different ways of picking \(f\) out of \(n\) nodes. \(\binom{n}{f}\) is pronounced “n choose f”, and it is defined as:

\[ \binom{n}{f} = \frac{n!}{f! \; (n-f)!} \]

Let \(r\) be the replication factor (typically \(r=3\)). If we assume that \(f\) out of \(n\) nodes have failed, what is the probability that a particular partition has all \(r\) replicas on failed nodes?

Well, in a system that uses consistent hashing, each partition is assigned to nodes independently and randomly (or pseudo-randomly). For a given partition, there are \(\binom{n}{r}\) different ways of assigning the \(r\) replicas to nodes, and these assignments are all equally likely to occur. Moreover, there are \(\binom{f}{r}\) different ways of choosing \(r\) replicas out of \(f\) failed nodes – these are the ways in which all \(r\) replicas can be assigned to failed nodes. We then work out the fraction of the assignments that result in all replicas having failed:

\[ P(\text{partition lost} \mid f \text{ nodes failed}) = \frac{\binom{f}{r}}{\binom{n}{r}} = \frac{f! \; (n-r)!}{(f-r)! \; n!} \]

(The vertical bar after “partition lost” is pronounced “given that”, and it indicates a conditional probability: the probability is given under the assumption that \(f\) nodes have failed.)

So that’s the probability that all replicas of one particular partition has been lost. What about a cluster with \(k\) partitions? If one or more partitions have been lost, we have lost data. Thus, in order to not lose data, we require that all \(k\) partitions are not lost:

\begin{align} P(\text{data loss} \mid f \text{ nodes failed}) &= 1 - P(\text{partition not lost} \mid f \text{ nodes failed})^k \\ &= 1 - \left( 1 - \frac{f! \; (n-r)!}{(f-r)! \; n!} \right)^k \end{align}

Cassandra and Riak call partitions “vnodes” instead, but they are the same thing. In general, the number of partitions \(k\) is independent from the number of nodes \(n\). In the case of Cassandra, there is usually a fixed number of partitions per node; the default is \(k=256\,n\) (configured by the num_tokens parameter), and this is also what I assumed for the graph above. In Riak, the number of partitions is fixed when you create the cluster, but generally more nodes also mean more partitions.

With all of this in place, we can now work out the probability of losing one or more partitions in a cluster of size \(n\) with a replication factor of \(r\). If the number of failures \(f\) is less than the replication factor, we can be sure that no data is lost. Thus, we need to add up the probabilities for all possible numbers of failures \(f\) with \(r \le f \le n\):

\begin{align} P(\text{data loss}) &= \sum_{f=r}^{n} \; P(\text{data loss} \;\cap\; f \text{ nodes failed}) \\ &= \sum_{f=r}^{n} \; P(f \text{ nodes failed}) \; P(\text{data loss} \mid f \text{ nodes failed}) \\ &= \sum_{f=r}^{n} \binom{n}{f} \, p^f \, (1-p)^{n-f} \left[ 1 - \left( 1 - \frac{f! \; (n-r)!}{(f-r)! \; n!} \right)^k \right] \end{align}

That is a bit of a mouthful, but I think it’s accurate. And if you plug in \(r=3\), \(p=0.001\) and \(k=256\,n\), and vary \(n\) between 3 and 10,000, then you get the graph above. I wrote a little Ruby program to do the calculation.

We can get a simpler approximation using the union bound:

\begin{align} P(\text{data loss}) &= P(\ge\text{ 1 partition lost}) \\ &= P\left( \bigcup_{i=1}^k \text{partition } i \text{ lost} \right) \\ &\le k\, P(\text{partition lost}) = k\, p^r \end{align}

Even though one partition failing is not independent from another partition failing, this approximation still applies. And it seems to match the exact result quite closely: in the graph, the data loss probability looks like a straight line, proportional to the number of nodes. The approximation says that the probability is proportional to the number of partitions, which is equivalent since we assumed a fixed 256 partitions per node.

Moreover, if we plug in the numbers for 10,000 nodes into the approximation, we get \(P(\text{data loss}) \le 256 \cdot 10^4 \cdot (10^{-3})^3 = 0.00256\), which matches the result from the Ruby program very closely.

And in practice…?

Is this a problem in practice? I don’t know. Mostly I think it’s an interesting and counter-intuitive phenomenon. I’ve heard rumours that it is causing real data loss at companies with large database clusters, but I’ve not seen the issue documented anywhere. If you’re aware of any discussions on this topic, please point me at them.

The calculation indicates that in order to reduce the probability of data loss, you can reduce the number of partitions or increase the replication factor. Using more replicas costs more, so it’s not ideal for large clusters that are already expensive. However, the number of partitions presents an interesting trade-off. Cassandra originally used one partition per node, but then switched to 256 partitions per node a few years ago in order to achieve better load distribution and more efficient rebalancing. The downside, as we can see from this calculation, is a much higher probability of losing at least one of the partitions.

I think it’s probably possible to devise replica assignment algorithms in which the probability of data loss does not grow with the cluster size, or at least does not grow as fast, but which nevertheless have good load distribution and rebalancing properties. That would be an interesting area to explore further. In that context, my colleague Stephan pointed out that the expected rate of data loss is constant in a cluster of a particular size, independent of the replica assignment algorithm – in other words, you can choose between a high probability of losing a small amount of data, and a low probability of losing a large amount of data! Is the latter better?

You need fairly large clusters before this effect really shows up, but clusters of thousands of nodes are used by various large companies, so I’d be interested to hear from people with operational experience at such scale. If the probability of permanently losing data in a 10,000 node cluster is really 0.25% per day, that would mean a 60% chance of losing data in a year. That’s way higher than the “one in a billion” getting-hit-by-an-asteroid probability that I talked about at the start.

Are the designers of distributed data systems aware of this issue? If I got this right, it’s something that should be taken into account when designing replication schemes. Hopefully this blog post will raise some awareness of the fact that just because you have three replicas you’re not automatically guaranteed to be safe.

Thank you to Mat Clayton for bringing this issue to my attention, and to Alastair Beresford, Stephan Kollmann, Christopher Meiklejohn, and Daniel Thomas for comments on a draft of this post.